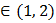Let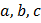 
be non-zero real numbers such that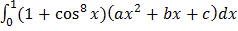 
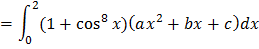
Then, the quadratic equation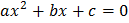 
has
a)
No root in (0, 2)
b)
At least one root in (1, 2)
c)
A double root in (0, 2)
d)
Two imaginary roots
Let 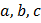be non-zero real numbers such that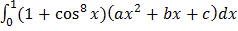
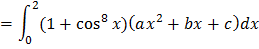
Then, the quadratic equation 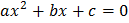has
a)
No root in (0, 2)
b)
At least one root in (1, 2)
c)
A double root in (0, 2)
d)
Two imaginary roots
Question ID - 100022 | SaraNextGen Answer
Let 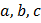be non-zero real numbers such that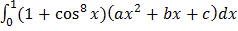
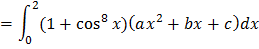
Then, the quadratic equation 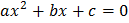has
a)
No root in (0, 2)
b)
At least one root in (1, 2)
c)
A double root in (0, 2)
d)
Two imaginary roots
|
Let
Then, the quadratic equation |
|||
|
a) |
No root in (0, 2) |
b) |
At least one root in (1, 2) |
|
c) |
A double root in (0, 2) |
d) |
Two imaginary roots |
1 Answer - 5876 Votes
3537
Answer Key : (b) -
Answer Link(b)
Consider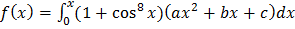 
Obviously,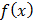 
is continuous and differentiable on [1, 2] and (1, 2) respectively.
Also,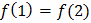 
(given)
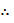By Rolle’s theorem there exist at least one point 
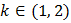such that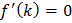 
Now,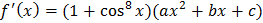 
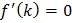
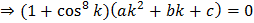
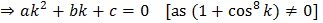
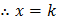is root of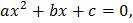 
Where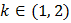 
Hence, at least one root 
