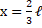An impulse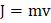 
at one end of a stationery uniform frictionless rod of mass 
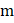and length 
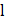which is free to rotate in a gravity-free space. The impact is elastic. Instantaneous axis of rotation of the rod will pass through
a)
Its centre of mass
b)
The centre of mass of the rod plus ball
c)
The point of impact of the ball on the rod
d)
The point which is at a distance 2/3 from the striking end
An impulse 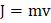at one end of a stationery uniform frictionless rod of mass 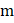and length 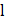which is free to rotate in a gravity-free space. The impact is elastic. Instantaneous axis of rotation of the rod will pass through
a)
Its centre of mass
b)
The centre of mass of the rod plus ball
c)
The point of impact of the ball on the rod
d)
The point which is at a distance 2/3 from the striking end
Question ID - 100096 | SaraNextGen Answer
An impulse 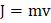at one end of a stationery uniform frictionless rod of mass 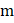and length 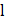which is free to rotate in a gravity-free space. The impact is elastic. Instantaneous axis of rotation of the rod will pass through
a)
Its centre of mass
b)
The centre of mass of the rod plus ball
c)
The point of impact of the ball on the rod
d)
The point which is at a distance 2/3 from the striking end
|
An impulse |
|
|
a) |
Its centre of mass |
|
b) |
The centre of mass of the rod plus ball |
|
c) |
The point of impact of the ball on the rod |
|
d) |
The point which is at a distance 2/3 from the striking end |
(d)
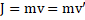
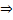Velocity of the CM of rod =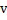
Applying impulse momentum equation about the CM of rod
.png)
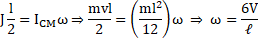
About instantaneous axis of rotation the rod is considered to have pure rotation
Let instantaneous axis of rotation be located at a distance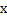 
from the colliding end
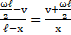…(i)
Substituting the value of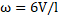 
in Eq.(i), we get 
