A cannon of mass 1000 kg located at the base of an inclined plane fires a shell of mass 50 kg in horizontal direction with velocity 180 km/h. The angle of inclination of the inclined plane with the horizontal is 
. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
a)
b)
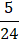
c)
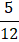
d)
None of these
A cannon of mass 1000 kg located at the base of an inclined plane fires a shell of mass 50 kg in horizontal direction with velocity 180 km/h. The angle of inclination of the inclined plane with the horizontal is . The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
a)
b)
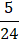
c)
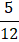
d)
None of these
Question ID - 100188 | SaraNextGen Answer
A cannon of mass 1000 kg located at the base of an inclined plane fires a shell of mass 50 kg in horizontal direction with velocity 180 km/h. The angle of inclination of the inclined plane with the horizontal is . The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
a)
b)
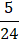
c)
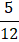
d)
None of these
|
A cannon of mass 1000 kg located at the base of an inclined plane fires a shell of mass 50 kg in horizontal direction with velocity 180 km/h. The angle of inclination of the inclined plane with the horizontal is |
|||||||
|
a) |
|
b) |
|
c) |
|
d) |
None of these |
(b)
Velocity of shell =180km/h=50m/s
Let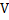 
be the velocity of the cannot after firing, then from the conservation of linear momentum,
.png)
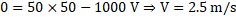
Let the cannot go up by height 
Net work done by external forces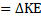 
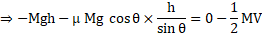
Where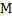 
is the mass of cannon,
Solving, we get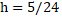 
m
