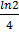At a given instant, say t = 0, two radioactive substance A and B have equal activities. The ratio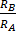 
of their activities after time t itself decays with time t as e−34 . If the half-life of A is m2 , the half-life of B is
|
a. |
|
b. |
2ln2 |
|
c. |
|
d. |
4ln2 |
Question ID - 50110 | SaraNextGen Answer At a given instant, say t = 0, two radioactive substance A and B have equal activities. The ratio 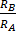of their activities after time t itself decays with time t as e−34 . If the half-life of A is m2 , the half-life of B is
a.
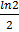
b.
2ln2
c.
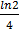
d.
4ln2
At a given instant, say t = 0, two radioactive substance A and B have equal activities. The ratio 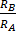of their activities after time t itself decays with time t as e−34 . If the half-life of A is m2 , the half-life of B is
|
a. |
|
b. |
2ln2 |
|
c. |
|
d. |
4ln2 |
1 Answer - 5876 Votes
3537
Answer Key : (c) -
Answer LinkHalf life of A = ln2
t1/2 =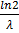 
λA = 1
at t = 0 RA = RB
NA e−λAT = NB e−λBT
NA = NB at t = 0
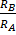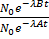
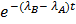at t = t 
= 
= e−t
λB−λA = 3
λB= 3 + λA = 4
t1/2 =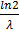 
= 
