The magnetic field associated with a light wave is given, at the origin, by B=B0[sin(3.14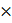 107)ct + sin(6.28
107)ct + sin(6.28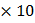 7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3
7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3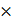 108ms−1,h=6.6
108ms−1,h=6.6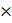 10−34 J-s)
10−34 J-s)
|
a. |
7.72eV |
b. |
8.52eV |
|
c. |
12.5eV |
d. |
6.82eV |
Question ID - 50156 | SaraNextGen Answer The magnetic field associated with a light wave is given, at the origin, by B=B0[sin(3.14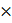 107)ct + sin(6.28
107)ct + sin(6.28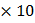 7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3
7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3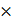 108ms−1,h=6.6
108ms−1,h=6.6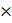 10−34 J-s)
10−34 J-s)
a.
7.72eV
b.
8.52eV
c.
12.5eV
d.
6.82eV
The magnetic field associated with a light wave is given, at the origin, by B=B0[sin(3.14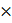 107)ct + sin(6.28
107)ct + sin(6.28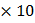 7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3
7ct). If this light gals on a silver plate having a work function of 4.7 eV, What will be the maximum kinetic energy of the photo electrons? (c=3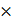 108ms−1,h=6.6
108ms−1,h=6.6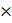 10−34 J-s)
10−34 J-s)
|
a. |
7.72eV |
b. |
8.52eV |
|
c. |
12.5eV |
d. |
6.82eV |
B1=B0sin(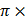 107C)t + B0 sin(2
107C)t + B0 sin(2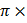 10−7C)t since there are two EM waves with different frequency, to get maximum kinetic energy we take the photon with higher frequency
10−7C)t since there are two EM waves with different frequency, to get maximum kinetic energy we take the photon with higher frequency
B1=B0sin(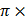 107C)t V1=
107C)t V1= 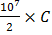
B2=B0sin(2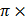 107C)t V2= 107C
107C)t V2= 107C
Where C is speed of light C=3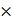 108 m/s
108 m/s
V2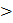 V1
V1
So KE of photoelectron will be maximum for photon of higher energy.
V2 =107CHz
hv= 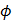 +KEmax
+KEmax
energy of photon
Eph=hv=6.6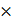 10−34
10−34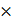 10−7
10−7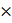 3
3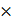 109
109
Eph=6.6 3
3 10−19J
10−19J
=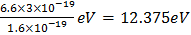
KEmax =Eph –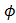
=12.375−4.7
=7.675eV 7.7 eV
7.7 eV
