Two stars of masses 3×1031kg each and at distance 2×1011m rotate in a plane about their common center of mass O. A meteorite passes through O moving perpendicular to the star’s rotation plane. In order to escape from the gravitational field of this star, the minimum speed that meteorite should have at O is: (Take Gravitational constant G=6.67×10−11 Nm2 Kg−2)
(a)
1.4×105 m/s
(b)
24 ×104 m/s
(c)
3.8 ×104 m/s
(d)
2.8 ×105 m/s
Two stars of masses 3×1031kg each and at distance 2×1011m rotate in a plane about their common center of mass O. A meteorite passes through O moving perpendicular to the star’s rotation plane. In order to escape from the gravitational field of this star, the minimum speed that meteorite should have at O is: (Take Gravitational constant G=6.67×10−11 Nm2 Kg−2)
(a)
1.4×105 m/s
(b)
24 ×104 m/s
(c)
3.8 ×104 m/s
(d)
2.8 ×105 m/s
Question ID - 50275 | SaraNextGen Answer
Two stars of masses 3×1031kg each and at distance 2×1011m rotate in a plane about their common center of mass O. A meteorite passes through O moving perpendicular to the star’s rotation plane. In order to escape from the gravitational field of this star, the minimum speed that meteorite should have at O is: (Take Gravitational constant G=6.67×10−11 Nm2 Kg−2)
(a)
1.4×105 m/s
(b)
24 ×104 m/s
(c)
3.8 ×104 m/s
(d)
2.8 ×105 m/s
|
Two stars of masses 3×1031kg each and at distance 2×1011m rotate in a plane about their common center of mass O. A meteorite passes through O moving perpendicular to the star’s rotation plane. In order to escape from the gravitational field of this star, the minimum speed that meteorite should have at O is: (Take Gravitational constant G=6.67×10−11 Nm2 Kg−2) |
|||
|
(a) |
1.4×105 m/s |
(b) |
24 ×104 m/s |
|
(c) |
3.8 ×104 m/s |
(d) |
2.8 ×105 m/s |
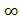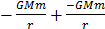By energy conservation between 0 &
.
+
mV2 =0+0
(M is mass of star m is mass of meteorite)
⇒ V =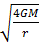
=2.8×105m/s
