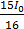An equilateral triangle ABC is cut from a thin solid sheet of wood, (see figure) D, E and F are the mid-points of its sides as shown and G is the center of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. It the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. then :
(a)
I=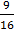 I0
I0
(b)
I= I0
I0
(c)
I=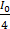
(d)
I=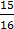 I0
I0
An equilateral triangle ABC is cut from a thin solid sheet of wood, (see figure) D, E and F are the mid-points of its sides as shown and G is the center of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. It the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. then :

(a)
I=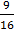 I0
I0
(b)
I= I0
I0
(c)
I=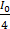
(d)
I=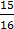 I0
I0
Question ID - 50298 | SaraNextGen Answer
An equilateral triangle ABC is cut from a thin solid sheet of wood, (see figure) D, E and F are the mid-points of its sides as shown and G is the center of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. It the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. then :

(a)
I=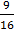 I0
I0
(b)
I= I0
I0
(c)
I=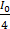
(d)
I=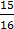 I0
I0
|
An equilateral triangle ABC is cut from a thin solid sheet of wood, (see figure) D, E and F are the mid-points of its sides as shown and G is the center of the triangle. The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane of the triangle is I0. It the smaller triangle DEF is removed from ABC, the moment of inertia of the remaining figure about the same axis is I. then :
|
|||
|
(a) |
I= |
(b) |
I= |
|
(c) |
I= |
(d) |
I= |
Suppose M is mass and a is side of larger triangle, then 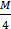 and
and  will be mass and side length of smaller triangle
will be mass and side length of smaller triangle
 ≈
≈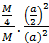
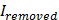 =
=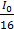
So, I=I0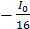 =
=